Quantum Cryptography Error Correction and Privacy Amplification: Observing the BB84 Protocol
Please note: This is an unpublished paper I wrote for my Master’s in May 2018. It does not involve any new research or findings on behalf of myself or anyone else. References are included, though not in any official format. I am sharing this upon request.
Abstract:
Classical cryptographic techniques will exist as the world’s method of encrypting information until quantum computers are successfully developed in conjunction with quantum algorithms. Current cryptographic techniques are not quantum-resistant; therefore, in a post-quantum world, all encrypted information will be vulnerable to anyone with a quantum computer. As a result, it is critical that quantum cryptographic techniques be developed so that quantum-resistant methods can be used to protect information, especially critically valuable information. Quantum Key Distribution (QKD) relies on the physical world, where the developed key is transmitted through photons. Because QKD depends on a third-party key developer (the QKD protocol) and physical means of sharing the key, key privacy must be dealt with in a drastically different way than how key privacy is dealt with in today’s public key cryptosystems. Physical variable state dependency means that learning about a QKD key through means of eavesdropping would result in changes to the key bits. Therefore, the key’s bits would not be received as expected, alerting the sender and receiver that someone had attempted to learn the key. In this paper, we will explore if and how exploiting eavesdroppers in the QKD process can be guaranteed. While it has been claimed that no undetected eavesdropping can occur, we will look at the BB84 protocol, exploring how error correction and privacy amplification are both necessary for a sender and receiver to end up with a truly secret key.
Introduction:
Public key cryptography as the world knows it has depended on the race to build a quantum computer. Whether or not quantum computers exist yet is not known, at least not by the public. Further still, a quantum computer is not useful in breaking cryptography unless it can be used to do so in ways different than non-quantum computers perform. Meanwhile, developing Quantum Key Distribution protocols is one of the most supported types of work regarding a proactive approach in information security, as the world knows it is only a matter of time before practically useful quantum computers appear. All information encrypted through non-quantum-resistant techniques will become public when quantum computing arrives and breaks all cryptography the world depends on today, which is often referred to as classical cryptography.
Currently, secure cryptographic systems are ensured due to the lack of ability for current computer capabilities to perform cryptanalysis against certain classical cryptographic techniques in a practical manner; these protocols simply cannot be broken quickly enough with existing computing power. As a specific example, the prime factors of the large numbers used as N in the RSA algorithm would take far longer than a lifetime to find through exhaustive attempts. Once quantum computers appear, this will no longer be the case.
Quantum cryptography is revolutionary in the cryptographic world because it offers a way to use quantum mechanics such that there is a lack of dependency upon key generation by the sender and receiver for use in an encrypted message exchange, and instead has the QKD protocol create the key to be used. As a result, the key cannot be found through the same cryptanalysis techniques used today in classical cryptography. In the cause of QKD, a malicious actor would eavesdrop on the activity between Alice (generally considered the message sender) and Bob (generally considered the message receiver) to learn about the key, but would fail to successfully do so without revealing herself.
The focus of this paper is how the concept of quantum states offer an evolution of cryptography, changing how cryptographic keys are produced and shared between two intended communicators.
QKD Protocols:
The idea behind Quantum Key Distribution is that quantum states of physical bits should be used as a means to transmit a cryptographic key. It should be noted that while these quantum states could be used to encrypt messages themselves, this cannot be done in a manner allowing the entire message to be received. As we will see later, error correction and privacy amplification of a key string depend on the string having room for subsets of bits to be removed. As a result, this technique is used for the key, not the message itself. We must also recognize that the bits used in QKD protocols are not the same single-state bits with which the world is familiar. Quantum techniques will use quantum bits, or qubits. Qubits do not have one, but two states. In the realm of quantum mechanics, we recognize that photons have both vertical and horizontal polarizations, in a sort of overlay manner. If the photon was in a bit form instead of qubit form, its state would be either horizontal or vertical, but as a qubit, its state has not yet been decided (3). This is important to understand because quantum mechanics expand beyond the normality expected of variable states, where something has but one state. Quantum mechanics not only shakes this reality, but relies on probabilities when understanding or predicting which states a variable is in. Photons have been specified here because in QKD protocols, a key is distributed over photons, typically over an optical fiber (5).
QKD is a manner of producing a cryptographic key through use of a cryptographic protocol relying on quantum mechanics. As opposed to either Alice or Bob generating a key, in the case of symmetric encryption, or both Alice and Bob generating her and his own key, in the case of asymmetric encryption, QKD has the quantum cryptographic protocol produce a key. The key can be used as a one-time pad, or as a shared, secret key between Alice and Bob (5). A one-time pad using a key generated by quantum cryptography would require that key bits be sent at the same (quick) rate as message bits, not making the one-time pad an ideal cryptosystem here (5). On the contrary, using QKD to produce a secret, shared key between Alice and Bob is quite an ideal cryptographic method.
Quantum measurements have been briefly mentioned in this paper thus far; we will now expand upon them. Quantum measurements are not passive actions (5). In fact, quantum measurements will generally result in changes to the quantum state of a variable (5). We say generally, because in the case that the outcome of a quantum measurement has been successfully predicted, the variable state will not change.
Now to be more specific in regards to quantum cryptography, this variable being measured is the signal, produced by the transmission of photons. Let us take a look at the basic QKD protocol, BB84, also known as the Bennet-Brassard Protocol. There are two important factors of cryptographic schemes to understand here. One, again from an eavesdropper standpoint, undetected eavesdropping cannot occur in this QKD because the photons’ states in the transmitted key will reflect whether an unintentional third-party listened in on the key transmission communication. Secondly, the fact of quantum measurements changing the photon’s states means that somehow Bob’s intended measurement of the key from Alice must not disturb the sharing of the key in that same manner as an eavesdropper. These are the most important aspects of BB84 to understand. The goals of the BB84 protocol are both to ensure knowledge of an eavesdropper and to make sure Alice’s exact message gets to Bob. The following section will expand on this protocol.
The Bennet-Brassard Protocol (BB84):
In classical cryptography, bits are sent over a channel in which an eavesdropper could potentially listen in on the communication without Alice or Bob knowing. If an eavesdropper found a way to intercept the communication, she could save each bite, copy it, and send it on to the destination, which in this case is Bob. Bob would still end up receiving Alice’s intended message, yet neither Alice or Bob would know an interceptor had read and copied the message simply based off of seeing what Bob received. BB84 essentially protects each bit being transmitted from being copied or seen by an eavesdropper because, as previously explained, of the physical state in which the bits are transmitted. Further, qubits cannot be copied. Because a qubit holds two states, the qubit’s state is decided after being measured, at which point it becomes but a bit.
As previously specified, QKD uses photons to transmit the key. Photons have two quantum variables, including polarization and momentum (5). The simpler of the two is polarization. The three states that a photon’s quantum polarization property can fall be described at a more abstract level as linear, circular, and elliptical (5). QKD deals with linear polarization, which in turn means that a qubit has both vertical polarization and horizontal polarization. Two-dimensional vectors are used to represent these linear polarization states (3). The photon’s states must be perpendicular (also referred to as orthogonal). Now, when measuring the state of the photon- which is the quantum object being used-, the photon can only be described has having one state. Each of the vectors in a set represents one of the two states that a photon could possible end up being described as being in, e.g. horizontal or vertical (4). This is where the qubit aspect of the photon comes in. The photon cannot be requested to describe what state it is in, but can say between two state options which state it is in. Again, however, this is not immediately known. As a qubit, the photon is currently holding two possible states. There is a process by which the photon can decide and respond with which state it is in.
The photon may technically be in one of the two states, or it may be in an in between state. This has not yet been decided though, which is why we earlier described the state as being overlay-like. In either case, it must decide between one state or the other. This may be done in a probabilistic manner. A basis is used to measure the qubit, causing one single state to be chosen. A orthonormal set is one in which two vectors are normalized and mutually perpendicular; an orthonormal basis acts as the measuring tool for the polarization of a photon in the case of the qubit (5). The photon’s state is decided by means of this basis, which returns whichever of the two possible states that the photon will take. As a result of taking a single state, the qubit becomes a bit.
BB84 takes this into account and in turn keeps track of Bob’s disruptive measurements such that Bob’s undisturbed data will be kept and all disturbed data will be discarded. Observe Figure A (who’s visualization technique has been borrowed from reference 5, Protecting Information):
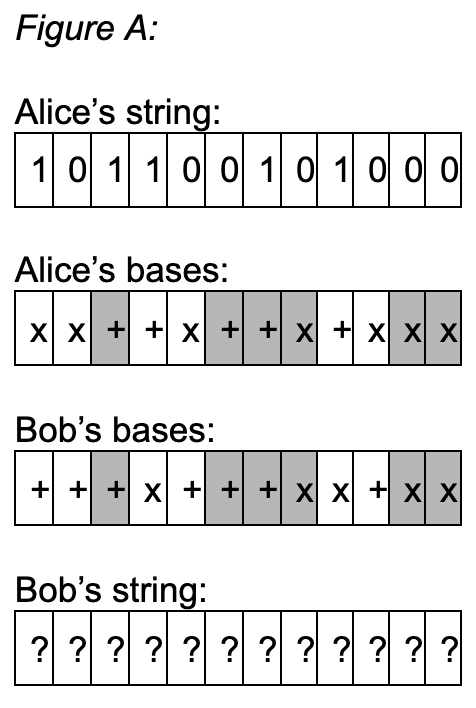
Figure A shows all the beginning ‘objects’ to be used in Alice and Bob’s key exchange using the BB84 protocol. Alice has her string that she wants to send to Bob. Bob does not know this string, and the goal is for him to learn it. Additionally, Alice and Bob will want Bob to be able to learn the key without an eavesdropper listening, but we will go more in depth into that later in the paper. For now, Alice and Bob each have their own bases. These bases are used for three reasons. They measure Alice’s qubits, alert Alice and Bob of an eavesdropper, and allow Alice and Bob to do error correction on the string that Bob ends up with.
The initial and most basic role of the bases is allowing the qubits to require a certain measurement in order to have the correct output state. Alice is using her bases as a way to hide the values of her key’s bits; this is the entire point of quantum cryptography, using physical properties and states to protect key sharing from eavesdroppers. By having her own decided bases for the qubits in her string, Alice will be sending over her sequence of qubits that will only be correctly deciphered if they are measured with the same bases by Bob (5). This means that Bob will be using his bases to determine what Alice has sent to him. This begs the question of how Bob can end up with Alice’s string if Alice and Bob do not know each other’s bases, but that will be explained.
BB84 Error Correction:
Following from the previous section, the bases will also be used for error correction. In classical cryptography, error correction is performed during a message’s transit. By using codewords in the midst of a channel’s extraneous noise, the message can be picked out. In quantum cryptography, however, error correction is done after, not during, a message is sent over a channel (5). This is because simply attempting to pick out specific parts of the noise could result in picking out noise that has been created by an eavesdropper.
After Bob has used his bases to measure the received photons, Alice and Bob will share their bases with each other over a public channel (5). Then, they will compare their strings- Alice her intended string and Bob his resulting string- with the other’s bases (5). Return to Figure A, where Alice and Bob’s matching bases have been highlighted. With each of them knowing the other’s bases, their last step will be to remove any bits which do not match the other’s (5). Because there is a 50% chance that Alice and Bob chose the same basis for any give qubit, it is likely that the final, error corrected string will be half of the original string length. When a qubit is measured with the incorrect base, it is not guaranteed to result in holding the expected state. However, the qubit still is not guaranteed to hold the expected state after being measured with the “correct” base. When a photon has taken neither a horizontal or vertical position, its end state is randomly chosen. This ends up affecting Bob’s chance of obtaining Alice’s string entirely correctly. In order to error correct Bob’s new string, a few more actions occur. Using a classical channel, Bob sends Alice his bases used in measuring her qubits (5). Alice responds by sending back the qubits that Bob measured correctly (5). Bob can do one last error correction, and finally ends up with Alice’s string.
Error correction becomes even more important for the third and last use of the bases, which is learning when an eavesdropper (who is generally referred to as Eve) has listened in on the key exchange. Remember that a measured qubit will become a bit, having lost its two-state property and become a bit with a single defined state. This causes even more trouble for Bob as he tries to receive Alice’s string and make sure they have the same key. Adding an eavesdropper into the mix means that during the process of Alice sending the qubits to Bob, Eve will act in a few ways. One, she will have to guess which basis she will use to measure each qubit. This then means that she will send on qubits, but with a certain amount of those qubits not having been measured correctly. More specifically, Bob will only receive 75% of the qubits as Alice intended (2). Half of the qubits will have been measured correctly, while the other half will not have been measured correctly. Within the qubits measured incorrectly, half of the randomly resulting state of those qubits will correct, therefore leading to Bob receiving 75% of the correct qubits (2). This can also be stated as Eve having a p/4 chance that she will cause an error in the bits (2). Thus, additional error correcting will need to be done in order to account for Eve’s actions.
Figure B (also based off of a figure in reference 5, Protecting Information) takes Alice and Bob’s strings and bases from before, and incorporates Eve’s actions into the resulting string that Bob ends up with. Eve’s randomly chosen bases sometimes impact Bob’s bit values, and sometimes don’t, due to the random choosing of a state that some bits sometimes do (recall that a photon needs to be in a horizontal or vertical state for the state to be chosen not at random; the photon cannot be at an in between state). For Eve to make an impact, she must have attempted to measure a qubit that Alice and Bob both used the same basis for. Otherwise, that bit has already been disposed of.
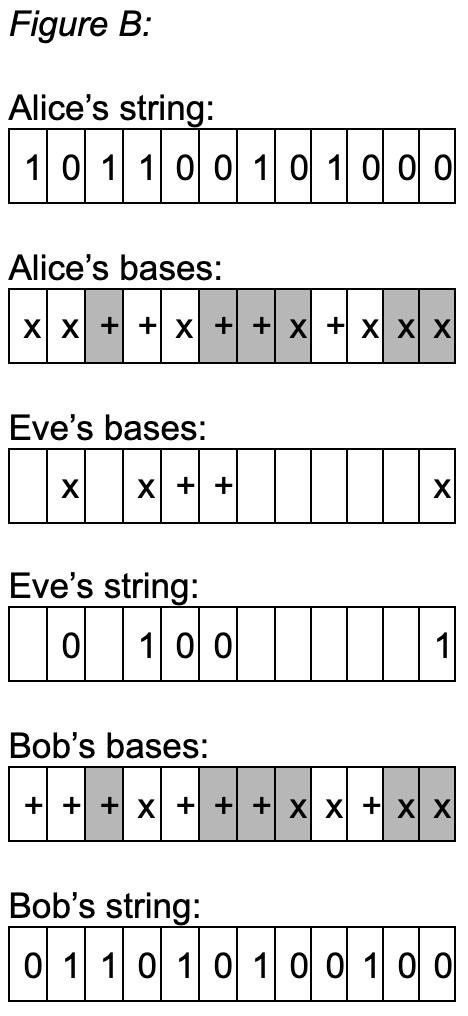
Alice and Bob can learn whether or not Eve was listening in on their communication by measuring a subset of their strings. It can be assumed that the strings are long enough such that sacrificing a portion of the strings will be okay. If those subsets match up 100%, Alice and Bob can assume that there was no interception of their key exchange. Otherwise, they can see what percent of their strings are not equivalent. They will discard the subset of the string that was sent over the classical channel and used to compare, and then will make their next derived strings even shorter. Using the knowledge of how much of the example string subset had errors due to Eve, they can assume their remaining string has about the same proportion of errors, and reduce their strings as needed in regards to that amount.
After Alice and Bob finish all necessary error correction steps, they must understand and deal with the amount of information that Eve has acquired throughout the entire process. This includes any information she found through listening in on the qubit communication, along with the information that Alice and Bob passed over their classical channel (5). Though that information itself hasn’t revealed anything to Eve, she will be able to put together certain amounts of information to an extent to which Alice and Bob should ensure will not affect their secret key exchange.
The randomness that occurs in measuring qubits can cause an issue when it comes to detecting and adjusting for any eavesdropping. When Bob receives a qubit, he measures it with the basis that he has chosen. When Eve is disturbing the message transmission, however, Bob cannot completely control whether or not his measurement takes her possibly state-changing actions into consideration (5). If Bob has happened to choose the incorrect basis for a qubit, then despite what Eve does, his measurement will later be detected as an error and thus thrown away (5). A problem arises when Eve has measured and tampered with the qubit now being sent to Bob, such that he uses the same basis as Alice. When Eve measures the qubit and changes the expected outcome of the qubit’s chosen state, Bob could get a false positive by thinking he correctly measured the qubit, when in reality he correctly measured Eve’s tampered qubit (5). As a result, when Alice and Bob are finding the error count in their final strings, they will not be able to see nor account for mistakes as such.
This means that there is a 1/2 probability of Eve causing an error when she makes the decision to measure a photon (5). Further, Eve’s overall probability of causing an error can be calculated as follows: 1/2 probability of measuring the photon 1/2 probability of causing an resulting error from said measurement Therefore, Eve’s total probability of causing an error is p/4.
Our look into error correction will end, with a transition into privacy amplification, with a higher level view at what is occurring during this process. There are two ways that error correction can occur. One, there can be one-way communication from Bob to Alice, where Bob makes decisions without having to receive feedback from Alice (5). Two, there can be two-way communication between Alice and Bob, which tends to be more efficient than the first option (5). An example of an interactive protocol is one that uses parity checks to fix errors (5). There are a few general rules that should be kept in mind in order to ensure that error correction through privacy amplification can work fully. One, the strings being used between Alice and Bob should start at a hefty length, as error correction can take a large toll on the amount of bits that will end up in the final strings (5). Additionally, the amount of errors that occur in their process should be taken into concern when they ultimately decide whether or not they were able to complete their process with a legitimately secret key. They must be careful in situations where a grandiose amount of errors have occurred because Eve already knows some information from her eavesdropping (5). Depending on the amount of knowledge she gained from her own findings, along with the information and strings sent over the classical channels by Alice and Bob to each other during the error correction process, Eve could be left with an amount of information that actually ends up being useful to her.
Privacy Amplification:
The purpose of privacy amplification is for Alice and Bob to ensure, to the best of their knowledge, that Eve has no information about the truly final strings that they end up with (5). In order to do so, they must figure out what information Eve does have, and then remove the chance of that knowledge allowing her to know anything about the key. This means that the length, n, of the strings directly depends on how much information Eve has learned (1). The information that Eve could find out includes a k amount of bits of the string, k parity checks of the string, what happens when Alice and Bob’s string is mapped to her k-bit string, and the string itself through a binary, symmetric channel (1).
The intent behind allowing Eve to have no knowledge of the final string is an attempt to reach Shannon’s definition of security, that specifies a plaintext p can have no correlation to its ciphertext c (1). Many quantum cryptographic protocols used for key agreement usually end up with partially known key information by a third-party, so it is common to rely on privacy amplification as a continued part of securing the shared key’s secrecy. Unconditionally secure protocols are often the goal, as the strongest proofs have no assumptions (1). This is the basis for many of the current two-party protocols used for privacy amplification.
There are two necessary parts for privacy amplification to be possible- one, the extent of Eve’s gained knowledge thus far must be removable, and Alice and Bob must have some knowledge about what information Eve has gained (1). Secret capacity of a broadcast channel allows Alice and Bob to transmit bits fast enough that it limits how much information Eve can get (1). Strong secret capacity allures to Eve being able to end up with a total amount of information considered to be arbitrarily small (1).
The steps and methods used in privacy amplification tend to be as follows. One, universal hashing, where a hash function is randomly chosen from a group of possible functions, is generally thought to be critical. Second, Rényi entropy, which is the amount of information not known about a bit, is an enormously important concept (5). It is often used, in the case of privacy amplification, such that we can describe Eve’s Rényi entropy throughout the process of making her knowledge negligible. If privacy amplification is successful, then Alice and Bob will end with a shared key that Eve is certain not to have any information about.
Errors in Error Correction:
It should be noted that there are many reasons as to why error correction will not be completed perfectly. For example, Alice and Bob do not measure their entire strings when finding the error rate; they take a subset of their strings and use that information to make a decision about the error rate for the entire string (this is, of course, because they send the subset over a classical channel and must throw it out afterwards; measuring the whole string would mean needing to throw out the entire string). This error rate is based off of proportions, and not actually finding every single error that must be accounted for. Another possible source of errors is the optical fiber itself, over which the photons are being sent. This fiber is likely imperfect, which will cause issues in itself (5). Further, there are more physical state errors that could occur. However, Alice and Bob will always assume any errors have been caused by an eavesdropper, and therefore these other potential causes have yet to impact the Alice and Bob’s transmission.
Continued and Future Work:
A few last aspects of quantum cryptography to consider, though they are not critical to this paper’s focus, are that while QKD protocols need not worry about transmission rate, distance is an issue. Today’s research is striving to push limits of these possible distances. In addition, while QKD protocols work either in theory or in the right physical setting, the physical settings can impede the ability of the protocol to follow through its expected actions. In fact, machines that use QKD protocols are sold and used today, but it has been a struggle for scientists and engineers to get physics in reality to act as physics on paper, i.e. in proofs, has worked. Because of this, it turns out that error correction seems to depend more on reality’s physical issues than on the qubits’ errors. This is, however, where the world stands today. If physical states are ever perfected, then error correction as explained in this paper will likely be considered a higher priority item to fix in given time.
Conclusion:
Quantum Key Distribution is a method of using quantum mechanics as a means of producing a secret, shared key. The BB84 protocol is a popular example of how QKD could work. More extensively, the BB84 protocol works to avoid an eavesdropper’s ability to listen in on a key distribution exchange without the sender and receiver knowing their key has been compromised. This is greatly important because if even a small fraction of a key is discovered, the entire key becomes incredibly vulnerable to a third party’s discovery.
In order to identify an eavesdropper’s presence, Alice and Bob must be able to exchange information, with the intention of Bob receiving Alice’s string, in a manner that identifies what unexpected actions have occurred. The interesting aspect of this exchange is that an eavesdropper is found due to measurements of qubit’s that lead to identified errors when the expected string and lack of errors was received. Yet, Bob must be able to measure the qubits that he receives and not let his measurements ruin his ability to receive the information that he needs. BB84 accounts for both needs- the lack of stealthiness by an eavesdropper, and a way for Bob to receive Alice’s string in a non-classical manner. Through error correction and privacy amplification, Alice and Bob are able to account for measurements by both Eve and Bob in a series of steps leading to Alice and Bob ending up with the same string, without any pieces of the key known by Eve. These two concepts have been shown to enable the two specified goals of BB84 to be reached.
References:
Bennett, C.h., et al. “Generalized Privacy Amplification.” IEEE Transactions on Information Theory, vol. 41, no. 6, 1995, pp. 1915–1923., doi:10.1109/18.476316.
Bennett, Charles H., and Gilles Brassard. “Quantum Cryptography: Public Key Distribution and Coin Tossing.” Theoretical Computer Science, vol. 560, 2014, pp. 7–11., doi:10.1016/j.tcs.2014.05.025.
Dür, Wolfgang, and Stefan Heusler. “The Qubit as Key to Quantum Physics Part II: Physical Realizations and Applications.” American Association of Physics Teachers, American Association of Physics Teachers, 2016, aapt.scitation.org/doi/10.1119/1.4897588.
Dür, Wolfgang, and Stefan Heusler. “Visualization of the Invisible: The Qubit as Key to Quantum Physics.” American Association of PhysicsTeachers, American Association of Physics Teachers, 2014, aapt.scitation.org/doi/10.1119/1.4897588.
Loepp, Susan, and William K. Wootters. Protecting Information: from Classical Error Correction to Quantum Cryptography. Cambridge University Press, 2006.